The Bisection Method is a numerical method for estimating the roots of a polynomial f(x). It is one of the simplest and most reliable but it is not the fastest method.
Problem: Here we have to find root for the polynomial x^3+x^2-1
Solution in C:
#include<stdio.h>
#include<math.h>
#define TOL 0.0001
float func(double x)
{
return (pow(x,3)+pow(x,2)-1);
}
int main()
{
double a,b;
int iteration,i;
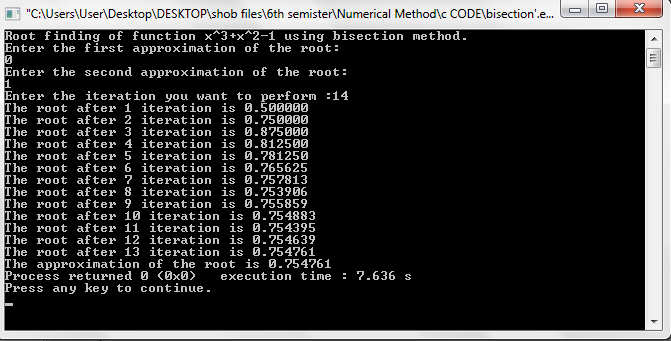
printf("Root finding of function x^3+x^2-1 using bisection method.\n");
printf("Enter the first approximation of the root:\n");
scanf("%lf",&a);
printf("Enter the second approximation of the root:\n");
scanf("%lf",&b);
printf("Enter the iteration you want to perform :");
scanf("%d",&iteration);
i=1;
double a1=a;
double b1=b;
double root,f1,f2,f3;
if(func(a1)==0)
root=a1;
else if(func(b1)==0)
root=b1;
else{
while(i<iteration)
{
root=(a1+b1)/2;
f1=func(a1);
f2=func(root);
f3=func(b1);
if(f2==0)
{
root=f2;
break;
}
printf("The root after %d iteration is %lf\n",i,root);
if(f1*f2<0)
b1=root;
else
if(f2*f3<0)
a1=root;
i++;
}
}
printf("The approximation of the root is %lf",root);
return 0;
}
Algorithm:
- Start
- Read a1, b1, TOL
*Here a1 and b1 are initial guesses
TOL is the absolute error or tolerance i.e. the desired degree of accuracy* - Compute: f1 = f(a1) and f3 = f(b1)
- If (f1*f3) > 0, then display initial guesses are wrong and goto step 11
Otherwise continue. - root = (a1 + b1)/2
- If [ (a1 – b1)/root ] < TOL , then display root and goto step 11
* Here [ ] refers to the modulus sign. *
or f(root)=0 then display root - Else, f2 = f(root)
- If (f1*f2) < 0, then b1=root
- Else if (f2*f3)<0 then a1=root
- else goto step 5
*Now the loop continues with new values.* - Stop
Output:
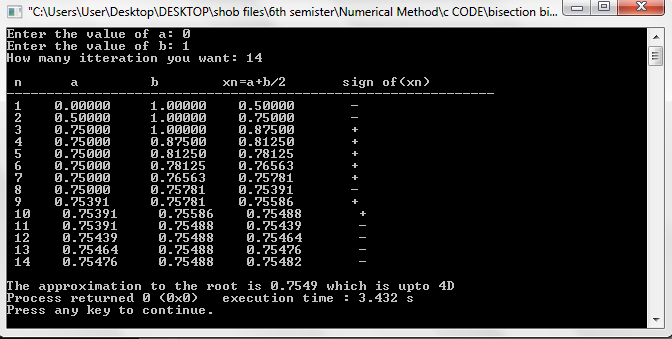
Another Problem Solving Code:
Problem: Here we have to find root for the polynomial x^3+x^2-1 upto 4D
#include<stdio.h>
#include<math.h>
#define f(y) (pow(x,3)+x*x-1);
int main()
{
double a,b,m=-1,x,y;
int n=0,k,i;
printf("Enter the value of a: ");
scanf("%lf",&a);
printf("Enter the value of b: ");
scanf("%lf",&b);
printf("How many itteration you want: ");
scanf("%d",&k);
printf("\n n a b xn=a+b/2 sign of(xn)\n");
printf("-------------------------------------------------------------\n");
for(i=1;i<=k;i++)
{
x=(a+b)/2;
y=f(x);
if(m==x)
{
break;
}
if(y>=0)
{
printf(" %d %.5lf %.5lf %.5lf +\n",i,a,b,x);
b=x;
}
else if(y<0)
{
printf(" %d %.5lf %.5lf %.5lf -\n",i,a,b,x);
a=x;
}
m=x;
}
printf("\nThe approximation to the root is %.4lf which is upto 4D",b);
return 0;
}