An equation ax2 + bx + c = 0 where a,b and c are any number and called the coefficient of the equation
It is known as quadratic equation because any seconbd degree polynomial equation is known as quadratic equation.This equation has two roots x1 and x2
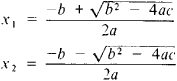
This is Bhaskara’s Formula or Bhaskaracharya’s Formula where discriminant D or Del = b2 − 4ac
If D>0 then root of quadratic equation are real and unequal
If D=0 then root of quadratic equation are real and equal
If D<0 then root of quadratic equation are conjugate complex number
Source:http://encyclopedia2.thefreedictionary.com/Bhaskaracharya%2
7s+Formula
http://www.wolframalpha.com/input/?i=Bhaskara%20formula
So my code is here
#include<iostream>
#include<cstdio>
#include<cmath>
int main()
{
double a,b,c,r1,r2,d;
scanf("%lf %lf %lf",&a,&b,&c);
d=(pow(b,2)-(4*a*c));
r1=(-b+sqrt(d))/(2*a);
r2=(-b-sqrt(d))/(2*a);
if(a!=0 && d>0)
{
printf("R1 = %.5lf\nR2 = %.5lf\n",r1,r2);
}
else{
printf("Impossivel calcular\n");
}
return 0;
}